


Next: Symmetry
Up: Program features of AOMX
Previous: Program features of AOMX
A Hamilton operator of the form
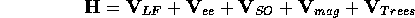
is applied. In the following, the individual terms and their
parametrization are explained in short; details can be taken from the given
literature.
-
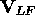 The ligand field is put up in the framework of
the Angular Overlap Model which is further described in
section B.1
The ligand field is put up in the framework of
the Angular Overlap Model which is further described in
section B.1 . For each ligand, the user supplies the
AOM parameters
. For each ligand, the user supplies the
AOM parameters 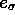 ,
, 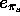 and
and 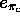 (eventually
(eventually
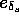 and
and 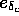 ) as well as the spatial oriention
in form of Eulerian angles
) as well as the spatial oriention
in form of Eulerian angles 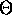 ,
, 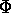 and (optional)
and (optional) 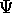 or
as a cartesian coordinate triple (x, y, z).
or
as a cartesian coordinate triple (x, y, z). The
The 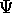 angle is relevant only in case of anisotropic
angle is relevant only in case of anisotropic
 -interaction (
-interaction ( 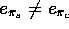 ), if required, it can be
calculated by the program through a plane to be supplied by the
user. Particularly in square planar complexes, the energetic effect
of a mixing in of the (n+1)s orbital becomes important and can be
covered through a parameter
), if required, it can be
calculated by the program through a plane to be supplied by the
user. Particularly in square planar complexes, the energetic effect
of a mixing in of the (n+1)s orbital becomes important and can be
covered through a parameter 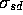 (see page
(see page
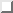 ). In chelate ligands with conjugated
). In chelate ligands with conjugated
 -electron system, the possibility exists to allow for the phase
coupling between the orbitals of the coordinating atoms of the
chelate; the AOM model then works with two
-electron system, the possibility exists to allow for the phase
coupling between the orbitals of the coordinating atoms of the
chelate; the AOM model then works with two 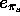 parameters,
parameters,
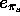 und
und 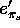 (p.
(p. ).
). -
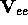 The operator of electron
repulsion is modeled through Racah parameters A, B and C.
The lowering of d electron interaction which is a consequence of
electron delocalization in the complex that generally occurs to a
different extent in the individual d orbitals, can be allowed for
through orbital reduction factors
The operator of electron
repulsion is modeled through Racah parameters A, B and C.
The lowering of d electron interaction which is a consequence of
electron delocalization in the complex that generally occurs to a
different extent in the individual d orbitals, can be allowed for
through orbital reduction factors 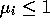 . The general
electron repulsion matrix element then takes the form
. The general
electron repulsion matrix element then takes the form 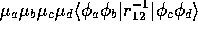 (see [4, 9]).
(see [4, 9]). -
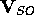 The spin-orbit coupling operator
has the form
The spin-orbit coupling operator
has the form 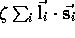 with the
parameter
with the
parameter 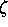 . Spatial anisotropy of orbital momentum is
introduced by the ansatz
. Spatial anisotropy of orbital momentum is
introduced by the ansatz 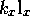 ,
, 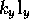 and
and 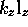 with parameters
with parameters 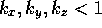 .[2]
.[2] -
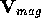 An external magnetic field is
described by the operator
An external magnetic field is
described by the operator 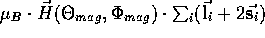 . Here, too, anisotropy can be accounted
for through parameters
. Here, too, anisotropy can be accounted
for through parameters 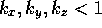 .
. -
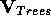 The Trees correction is
a two-electron correction of the form
The Trees correction is
a two-electron correction of the form 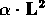 (see
[5] and [1]) with the Trees parameter
(see
[5] and [1]) with the Trees parameter
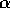 .
.



Next: Symmetry
Up: Program features of AOMX
Previous: Program features of AOMX
Heribert Adamsky
Sat Sep 14 16:23:16 MET DST 1996
![]()
![]()